6.28

The polynomial f(x) = 0.0074*x^4 - .284*x^3 + 3.355x^2 - 12.183*x +5 has areal root between 15 and 20. Apply the Newton- Raphson method to this function using an initial guess of x_0 = 16.15. Explain your results. 


Matlab code

p = [0.0074 -.284 3.355 -12.183 5];

x_i = [15:0.001:20];

f = @(x) 0.0074*x .^4 - .284*x .^3 + 3.355 *x .^2 - 12.183*x + 5;

hold on

plot(x_i, polyval(p,x_i))

plot(x_i, polyval(polyder(p),x_i), 'r')

%x_0 = 16.5;%bad

x_0 = 18;%good

k = polyder(p);

for ii =1:100

     plot(x_0 ,f(x_0),'*g')

    x = x_0 - (polyval(p,x_0) ./ polyval(k,x_0));

    x_0 = x;

end

Results:

Using the specified initial guess of 16.5, Newton-Raphson diverges badly

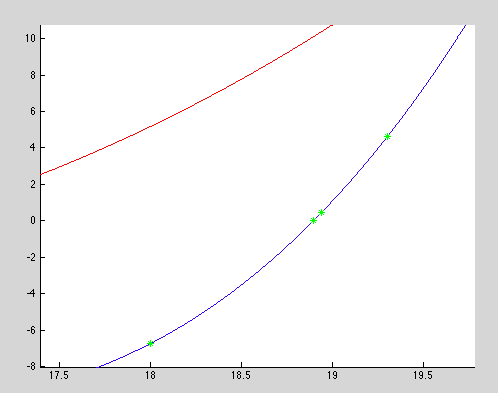
Using an initial guess of 18, a little farther through the test range, it converges much more nicely

x =

   18.8948

EDU>> f(x)

ans =

  -5.6843e-14

The real root is at 18.8948. Plugging it back into the equation results in -5.6843e-14, which is negligible from 0